Algorithm Challenges #1
Leetcode Weekly Contest 406
1. Lexicographically Smallest String After a Swap
Link: https://leetcode.com/problems/lexicographically-smallest-string-after-a-swap/
This problem states that I should find the minimum number represented in a string by swapping at most once. One restriction is that I can swap two characters if those have the same parity. It just means that I can only choose two odds or even numbers, not both simultaneously.
I have two options: swap or do not swap. If I swap, I should find adjacent characters that meet the following conditions.
Both
s[i-1]ands[i]should be odd or even. I can detect it by subtracting two numbers and getting modulo by 2. It should be 0 if those have the same parity.The number
s[i-1]should be greater because it can make the current string smaller.
If any position i meets the conditions above, then I can just return the result after swapping s[i] and s[i-1]. Otherwise, I can return the input.
Here’s my code.
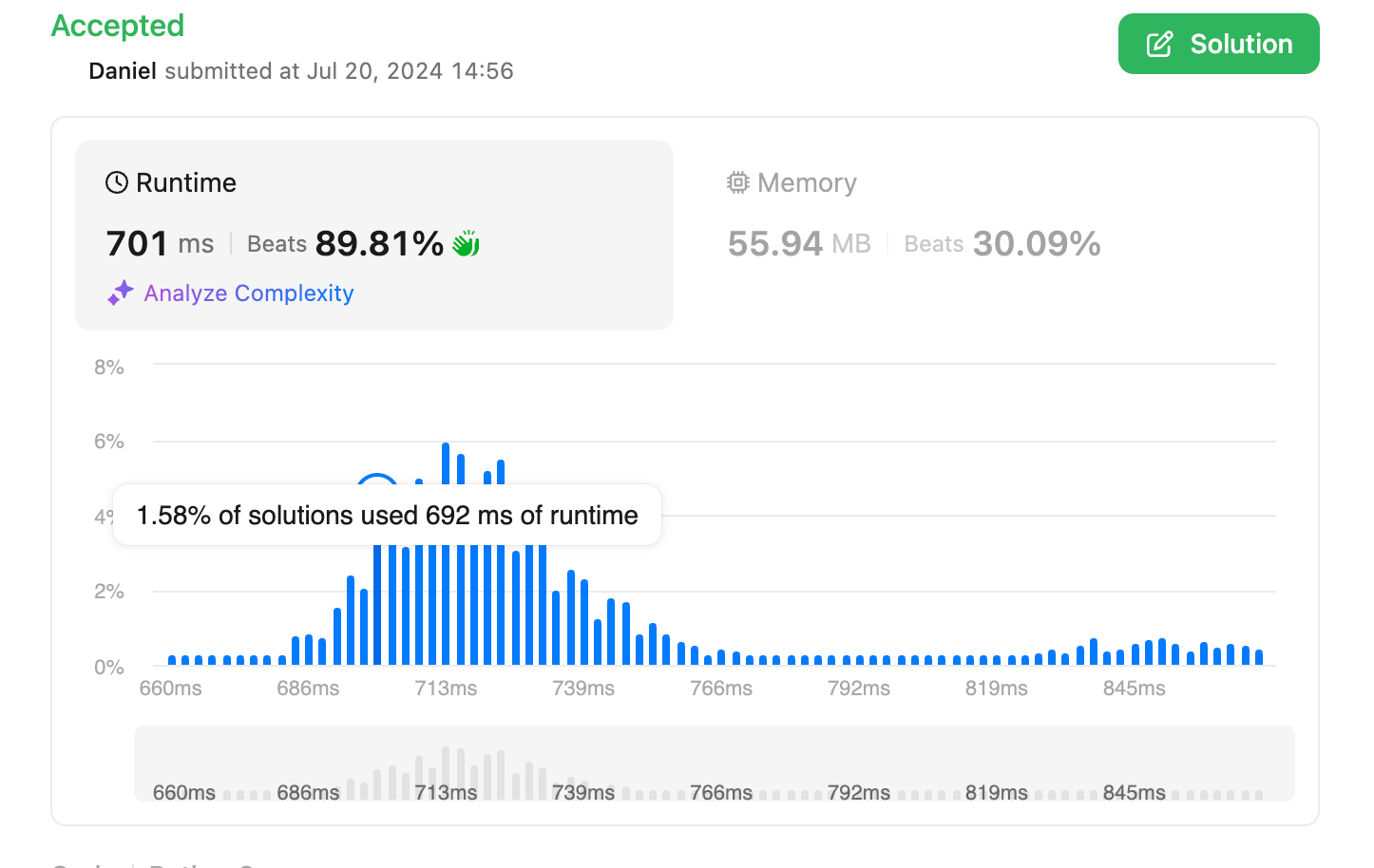
Time complexity should be O(N), where N is the length of s. It’s because I iterate the whole characters.
Space complexity should be O(1) because I do not assign any variables that consume memory more than O(1).
class Solution:
def getSmallestString(self, s: str) -> str:
n = len(s)
for i in range(1, n):
ni, np = int(s[i]), int(s[i-1])
if ni < np and (np - ni) % 2 == 0:
swapped = s[:i-1] + s[i] + s[i-1] + s[i+1:]
return swapped
return s2. Delete Nodes From Linked List Present in Array
Link: https://leetcode.com/problems/delete-nodes-from-linked-list-present-in-array/
This problem is a typical question we can face when we learn the two-pointer technique. Two-pointers is the algorithm technique in which you can use two different pointers, usually faster and slower, to iterate all nodes.
I usually add a dummy node with the head as the next node because the head node can be deleted or changed according to the situation. If you have a dummy node, you don’t need to think about the case where the head gets None. When you return the actual head, then return the dummy.next which can be None.
Also, I changed the numbers list to a set because it can be duplicated. A set is implemented with a hash table to provide the O(1) membership operation. If you use the nums array while iterating the nodes, you should add O(N) time complexity in each iteration. But if you change it to set, it would be O(1).
Here’s my code.
Time complexity is O(N), where N is the bigger one between the number of elements in nums and nodes.
Space complexity can be O(N) because I use a set container. Even though I override the variable name, I’m not sure it could remove N spaces while running this code internally.
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def modifiedList(self, nums: List[int], head: Optional[ListNode]) -> Optional[ListNode]:
nums = set(nums)
dummy = ListNode(next=head)
prev, curr = dummy, head
while curr:
_next = curr.next
if curr.val in nums:
# Remove the current node
prev.next = _next
else:
prev = curr
curr = _next
return dummy.nextIf you do not change nums to set type, then you cannot pass.
class Solution:
def modifiedList(self, nums: List[int], head: Optional[ListNode]) -> Optional[ListNode]:
# nums = set(nums) <- comment this line to check the result.
dummy = ListNode(next=head)
prev, curr = dummy, head
while curr:
_next = curr.next
if curr.val in nums:
# Remove the current node
prev.next = _next
else:
prev = curr
curr = _next
return dummy.next3. Minimum Cost for Cutting Cake I
Link: https://leetcode.com/problems/minimum-cost-for-cutting-cake-i/description/
This problem states that I should minimize the code to cut cakes into 1x1 pieces. I first focused on what would happen if I cut the cake vertically or horizontally. If I cut the cake vertically, then the piece becomes two smaller pieces. Also, I cannot cut the whole cake with a long knife. This means that if I decide to cut a specific line, I should cut as many times as the pieces with that line.
So, I keep track of vertical and horizontal pieces to calculate the overall cost of cutting a specific line. If I decide to cut a vertical line x, I should cut as many times as the horizontal pieces, which will cost verticalCut[x] * horizontal_pieces. Also, If I cut a vertical line, the number of vertical pieces increases by 1 because all of the pieces are cut in half.
Until now, I just discovered what would happen if I cut the cake. Now, I must decide where to cut first to minimize the overall cost. As I can’t reduce the cost by cutting multiple cakes, I just need to pay as much as I cut a cake. So, I need to reduce the cost by reducing the pieces of cake I should cut with the high cost. It means that I should cut the line that has the higher cost. If I cut the line that costs smaller, I should pay more cost when I cut the line that has higher cost because it must have more pieces to cut made from the previous cuts.
Here’s the code.
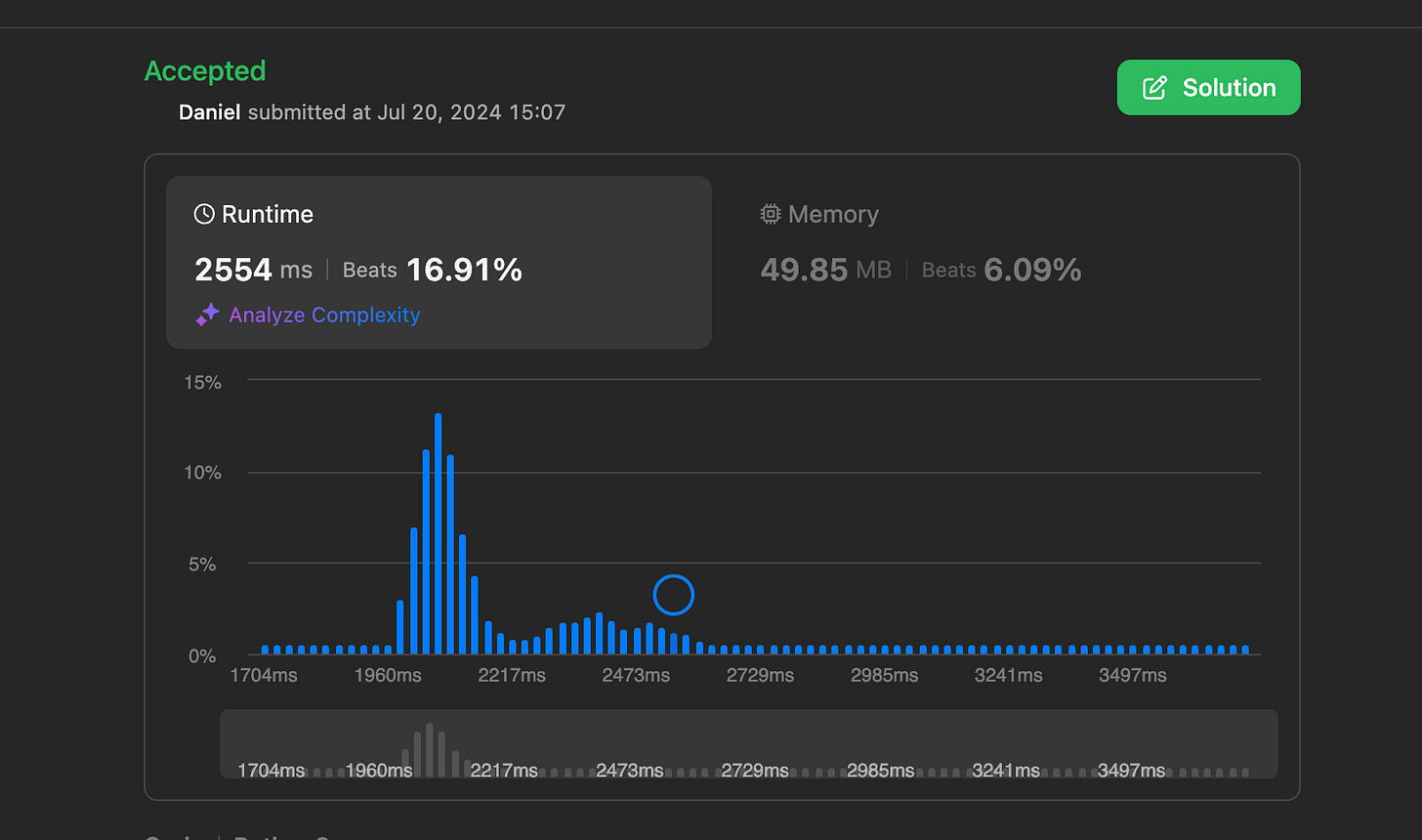
Time complexity is O((M + N)log(M+N)), where M is the length of horizontalCut, N is the length of verticalCut. Sorting the list costs more than iteration.
Space complexity is O(M+N) because I assigned another list to store the horizontalCut and verticalCut.
class Solution:
def minimumCost(self, m: int, n: int, horizontalCut: List[int], verticalCut: List[int]) -> int:
arr = [ (hc, 1) for hc in horizontalCut ] + [ (vc, 0) for vc in verticalCut ]
arr.sort(key=lambda x: -x[0])
ans = 0
v_cnt = h_cnt = 1
for cost, d in arr:
if d == 0:
# cut vertically
ans += cost * h_cnt
v_cnt += 1
else:
ans += cost * v_cnt
h_cnt += 1
return ans4. Minimum Cost for Cutting Cake II
https://leetcode.com/problems/minimum-cost-for-cutting-cake-ii/description/
This is literally the same question with the problem3 but the value of m and n is larger. But it doesn’t matter. The time complexity and space complexity that I provided with the code meets the constraints.